In this page we will learn how to easily plot vector fields with SageMath.

We will use the function plot_vector_field for a vector field in \(\mathbb{R}^2\) and the function plot_vector_field3d for vector fields in \(\mathbb{R}^3\).

Example 1

We will plot the vector field from our first example in the Vector Fields page:

\[\mathbf{F}(x,y) = \langle 1,0 \rangle\]

This is a constant vector field that assigns the vector \(\langle 1,0\rangle\) to each point in the plane.

We define the vector field with

F(x,y) = [ 1, 0 ]

Then, we plot the vector field with

plot_vector_field(F,(x,-3,3),(y,-3,3),aspect_ratio=1)

This will produce the figure

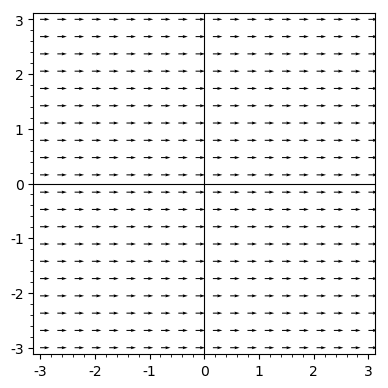
Vector field

Notice that we used the option aspect_ratio=1 to produce a squared figure.

Example 2

In this example we will plot the vector field \(\mathbf{F}(x,y) = \langle x, x^2\rangle\).

We will use the same function above.

F(x,y) = [ x, x^2 ]
plot_vector_field(F,(x,-2,2),(y,-2,2),aspect_ratio=1)

The previous command produces the figure below:

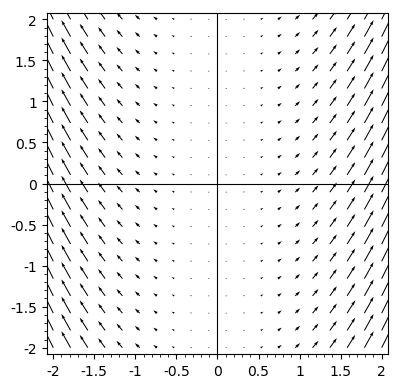
Vector field


Example 3

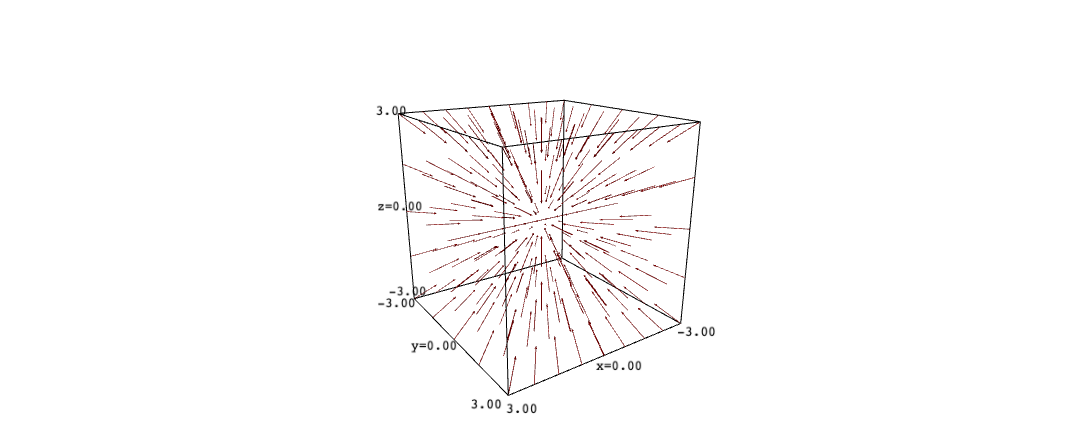
In this example we will plot a vector field in \(\mathbb{R}^3\)

\[\mathbf{F} = -\frac{1}{r}\langle x,y,z\rangle\]

where \(r = \sqrt{x^2+y^2+z^2}\).

If we attempt to run the plot_vector_field3d function the same way we use plot_vector_field we will end up with an error:

y, z = var('y,z')
r(x,y,z) = sqrt(x^2+y^2+z^2)
F = [ -x/r, -y/r, -z/r ]

plot_vector_field3d(F,(x,-3,3),(y,-3,3),(z,-3,3),aspect_ratio=1)

RichReprWarning: Exception in _rich_repr_ while displaying object: 
array must not contain infs or NaNs

The issue we are facing is that our vector field is not defined at the point \((0,0,0)\).

To solve this problem, we will use two plots: one of them setting the range of \(x\) at \((-3,-0.01)\) and the other one at \((0.01,3)\):

G1 = plot_vector_field3d(F,(x,-3,-0.01),(y,-3,3),(z,-3,3),aspect_ratio=1)
G2 = plot_vector_field3d(F,(x,0.01,3),(y,-3,3),(z,-3,3),aspect_ratio=1)

Then we can show the two plots combined using

show(G1+G2)

The figure below shows the corresponding output (we rotated the figure for a better perspective):

Vector field